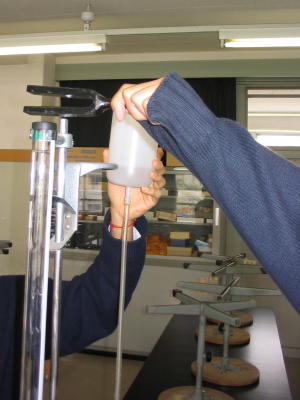
気柱の共鳴
目的
- 気柱共鳴装置を使って音さの振動数を測定する。閉管にできる音波の定常波について理解を深める。
〔原理〕
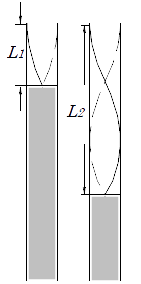 閉管の管口付近で音さをならしたとき、音さの振動数と管の固有振動数が等しければ、管内には定常波ができ、共鳴が起きる。
閉管の管口付近で音さをならしたとき、音さの振動数と管の固有振動数が等しければ、管内には定常波ができ、共鳴が起きる。- 気柱共鳴装置で水面を上下させ、基本振動、3倍振動、(あるいは5倍振動)が起きる場所を測定することによって、音さの振動数を計算することができる。
- 管口は自由端反射、水面は固定端反射と考えることができるので、管口付近は定常波の腹になり、水面の位置は節になる。なお、管口がちょうど腹の位置にはならないことに注意する。
準備
方法
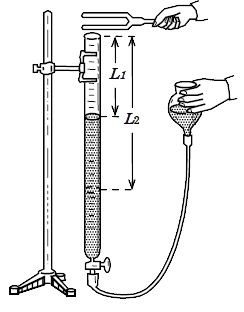 実験室の温度を測定する。(t1 )
実験室の温度を測定する。(t1 )- 気柱共鳴装置の水カップを管口のあたりで支え、ガラス管内に水を入れる。水面の位置は、ガラス管の方は管口近く、水カップの方は底の近くになるようにする。
- 音さを槌でたたき、管口に近づける。
- 水カップをゆっくり下げていくと、ガラス管内の水面も下がっていく。水面を下げながら、気柱が共鳴して音さの音が大きく聞こえる点を探し、その付近を何度か上下させて、ガラス管の管口から水面までの距離L1を求める。(目盛の読み取りは3回行い、その平均を求める)
- さらに水カップをゆっくり下げていき、2回目の共鳴点を探し、同様にガラス管の管口から水面までの距離L2を求める。(目盛の読み取りは3回行い、その平均を求める)
- 管の内径を測る。また、最後にもう一度実験室の温度を測定する。(t2 )
処理
- 波長を次の式より求める。 λ=2(L2-L1)
- 実験室の平均温度tを求め、V=331.5+0.6t より音の速さV[m/s]を求める。
- 音さの振動数f[Hz]をV=fλより求める。
結果
〇実験室の温度
| はじめ |
t1=15.8 [℃] |
| おわり |
t2=16.2 [℃] |
| 平均 |
t=16.0 [℃] |
〇共鳴点の測定
| 回数 |
1 |
2 |
3 |
平均 |
| L1 [m] |
0.115 [m] |
0.120 [m] |
0.119 [m] |
0.118 [m] |
| L2 [m] |
0.370 [m] |
0.376 [m] |
0.370 [m] |
0.372 [m] |
- ○波長λの計算
- 式 λ=2 ( 0.372 - 0.118 ) = 0.508 [m]
- ○音の速さVの計算
- 式 V= 331.5 + 0.6 × 16 = 341.1 [m/s]
- ○音さの振動数の計算
- 式
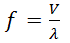 = 341.1 / 0.508 = 671 [Hz]
= 341.1 / 0.508 = 671 [Hz]
考察
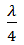 とL1との差から定常波の腹の位置が、開口端より何cm上にあるか求める。 (これを開口端補正という)
とL1との差から定常波の腹の位置が、開口端より何cm上にあるか求める。 (これを開口端補正という)
λ/4 - L1 = 0.127 - 0.118 = 0.009 = 0.90 [cm]
- 開口端補正⊿Lは管の内径dのおよそ何倍になるか。
0.90 ÷ 2.8 = 0.32 倍
開口端補正は一般に管の半径の0.60~0.65倍になると言われている。
- 温度が高くなると、L2,L1の値はどのように変化するか。
温度が高くなると音の速さVは大きくなる。振動数fは変化しないので、λが大きくなる。よって、L2,L1は長くなる。
- 管楽器の音の高さは気温が高いときどのように変化すると考えられるか。
温度が高くなると音の速さVは大きくなる。管楽器の長さが変わらないとλは変わらない。よって、振動数fが大きくなり、音程は高くなる。
実験プリントpdfファイル





 閉管の管口付近で音さをならしたとき、音さの振動数と管の固有振動数が等しければ、管内には定常波ができ、共鳴が起きる。
閉管の管口付近で音さをならしたとき、音さの振動数と管の固有振動数が等しければ、管内には定常波ができ、共鳴が起きる。 実験室の温度を測定する。(t1 )
実験室の温度を測定する。(t1 )