バネ振り子の周期
目的
- フックの法則を検証し、バネ定数 k の値を求める。また、おもりをつるして上下に振動させたときの周期が
T=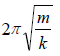 になることを確かめる。
になることを確かめる。
準備
- つるまきバネ,スタンド,ものさし,10gのおもり (5個くらい),ストップウォッチ
方法
実験.I つるまきバネのバネ定数kの測定
 バネの一端をスタンドに固定し、バネが鉛直になるように調整する。バネにそってものさしを固定し、バネの下端に位置L0を読み取る。
バネの一端をスタンドに固定し、バネが鉛直になるように調整する。バネにそってものさしを固定し、バネの下端に位置L0を読み取る。- バネにおもりを1個,2個,3個,・・・とつるしていき、バネの下端の位置L1,L2,L3,・・・を読み取る。最後のおもりをつるして測定した後、逆におもりを1個ずつ減らしていき、バネの下端の位置を読み取っていき、2つの値の平均を求める。(視線がものさしに垂直になるようにして目盛を読むこと)
- バネの伸びxnおよびおもりにはたらく重力Fを計算する。
- バネの伸びxnとおもりにはたらく重力Fの関係をグラフにし、その傾きからバネ定数k[N/m]を求める。
実験.II バネ振り子の周期の測定
- つるまきバネに質量m[kg]のおもりをつるして、上下に振動させ、10往復の時間を測定する。
(振動の中心に目印をつけ、おもりが目印を上から下へ通過するたびにカウントすればよい)
- 10往復の時間から周期Tを求める。
- 実験Iで求めたkの値を用いて、公式T=
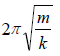 から理論値を計算し、実験から求めた値と比較する。
から理論値を計算し、実験から求めた値と比較する。
結果
<実験I>
実験I 測定結果
m
×10-3[kg] |
Ln×10-2[m] |
xn(=Ln-L0)
×10-2[m] |
F(=mg)
×10-3[N] |
| Ln |
1回 |
2回 |
平均 |
| 0 |
L0 |
13.0 |
13.0 |
13.0 |
0 |
0 |
| 10 |
L1 |
15.4 |
15.6 |
15.5 |
2.5 |
98 |
| 20 |
L2 |
18.2 |
18.4 |
18.3 |
5.3 |
196 |
| 30 |
L3 |
21.1 |
21.3 |
21.2 |
8.2 |
294 |
| 40 |
L4 |
24.0 |
24.1 |
24.1 |
11.1 |
392 |
| 50 |
L5 |
26.9 |
26.9 |
26.9 |
13.9 |
490 |
表の結果からグラフを作成する。
 ◆グラフの傾き k=3.43[N/m]
◆グラフの傾き k=3.43[N/m]
実験II
周期の実験値と理論値[s]
おもりの質量m
[×10-3kg] |
1回 |
2回 |
3回 |
実験値平均 |
理論値 |
相対誤差 |
| 20 |
0.505 |
0.500 |
0.500 |
0.502 |
0.480 |
(0.502-0.480)/0.480=4.6% |
| 30 |
0.609 |
0.607 |
0.611 |
0.609 |
0.588 |
(0.609-0.588)/0.588=3.6% |
| 40 |
0.693 |
0.700 |
0.694 |
0.696 |
0.679 |
(0.696-0.679)/0.679=2.5% |
考察
- 周期の理論値と実験値との誤差について考察する。
おもりの上下振動のぶれ、バネのねじれ、おもりの回転、空気抵抗などの影響で周期の実験値は理論値よりも長くなると思われる。
また、これらによって力学的エネルギーが減少するためバネの振動はしだいに減衰していくと考えられる。
おもりの質量が大きく周期が長い方が相対誤差が小さいことから、1秒間の振動数が多いほどエネルギーの減少も大きいことがわかる。
- この実験で興味関心・疑問を持った点、今後の課題などについて
実験プリントpdfファイル





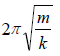 になることを確かめる。
になることを確かめる。 バネの一端をスタンドに固定し、バネが鉛直になるように調整する。バネにそってものさしを固定し、バネの下端に位置L0を読み取る。
バネの一端をスタンドに固定し、バネが鉛直になるように調整する。バネにそってものさしを固定し、バネの下端に位置L0を読み取る。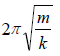 から理論値を計算し、実験から求めた値と比較する。
から理論値を計算し、実験から求めた値と比較する。

 ◆グラフの傾き k=3.43[N/m]
◆グラフの傾き k=3.43[N/m]